TECHNICAL, FUNDAMENTAL & INTERMARKET ANALYSIS USING AI

Chapter 5

Synergistic Market Analysis: Combining Technical, Fundamental, and
Intermarket Analysis Using Artificial Intelligence

By Louis B. Mendelsohn

INTRODUCTION
Recent advancements in telecommunications and computing technologies — often referred to as the “information technology revolution” — coupled with the emergence of derivative instruments, including futures and options, have brought about the globalization of the world’s financial markets. Now there is nearly instantaneous worldwide communication and on-line linkages between exchanges along the emerging information or “electronic” superhighway. The effects of this are best exemplified by the 1987 stock market crash, which can be considered the first instance of a truly global financial market phenomenon.

Now, even a casual reader of a daily newspaper or viewer of the nightly news is aware that the world’s markets and economies influence each other on a daily basis in an interconnected web of cause and effect. No longer independent, today’s financial markets are now synergistically linked to one another.

Additionally, the proliferation of trading markets in emerging growth regions of the world — including the Pacific Rim, Asia and Latin America — has contributed to this global interdependence. This trend, which is both unprecedented and irreversible, has serious implications for traders who want to profit from global trading opportunities in the 1990s.

Other Factors Contribute To Market Globalization
The globalization of the financial markets has been further accelerated by other related factors, which include the diminished influence of the G7 western nation central banks in controlling interest and foreign exchange rates, cross-border consolidation of corporations into multinational entities, increased trade by emerging nations, the listing of corporate shares concurrently on multiple exchanges, and the needs of corporate and financial institutions to manage risk on a twenty-four hour worldwide basis.

The Result: Market Globalization
Global trading is now conducted around the clock by most major financial institutions. By the end of this century the world’s financial markets will coalesce into one global market, while each of the individual markets that traders are focusing on today will simply be components or different facets of that one market.

Globalization has altered the character and nature of the world’s financial markets, in terms of how they behave and interact. The global markets of the 1990s offer unprecedented trading opportunities. Yet, most traders have given little thought to the implications that globalization will have on their trading, particularly during an acute financial crisis in terms of illiquidity and counter-party risk. Most traders continue to focus entirely on one market at a time, failing to implement any sort of intermarket analysis or global perspective in their trading. They are content to ignore the intermarket global context through which all financial markets are now linked to one another as component parts of a larger whole.

This is a very serious and potentially costly oversight, since single-market analysis, due to its narrow inward focus, cannot discern the underlying force or market synergy in today’s globally interrelated markets. Now, new analytic methods are a sine qua non for profitable trading. They must be capable of identifying hidden patterns and discovering relationships in disparate data.

Broader Market Analysis is Needed
Traders need to adapt their trading strategies and methods, in order to survive and profit in this new world order. Today’s limited single-market focus must yield to a broader analytic framework that can quantify complex intermarket relationships. What is needed for successful trading is a broader concept of market analysis that recognizes the nonlinear interrelatedness and interdependence of today’s financial markets. Traders can no longer focus solely on individual markets. It is now imperative that they adopt an intermarket trading perspective and utilize analytic tools capable of assessing complex intermarket relationships. To accomplish this, traders must expand their analytic perspective to include external factors in addition to internal factors that affect a given market. It is this broader synergistic context that must become the focus of market analysis for successful trading in the 1990s.

Technical market analysis must encompass the global context of today’s financial markets, by incorporating the more narrowly defined schools of technical, fundamental, and intermarket analysis as they are presently practiced (See Figure 1). I refer to this more comprehensive method of analysis as Synergistic Market Analysis (SMA). This approach utilizes various mathematical technologies, including neural networks, to quantify relationships and find hidden patterns between related financial markets. By doing so, it allows traders to capture and act upon information reflecting the market synergy that drives today’s markets.

SYNERGISTIC ANALYSIS

Background
In 1983, when I introduced single-market historical simulation and back-testing in microcomputer software and developed ProfitTaker, the first commercial PC-trading software with this capability, most technical analysis was performed manually or with primitive software programs. By the mid-1980s historical testing had become the backbone of computerized technical analysis, with the emergence of a software industry catering to individual computerized traders.

Yet, as I surmised the likely effect that market globalization would have on technical analysis and trading, it was apparent that single-market analysis alone would no longer be adequate. With formerly isolated markets now interconnected, new analytic approaches would be required for profitable trading.

In 1987, I developed trading software that used a spreadsheet format to correlate the effects of intermarket and fundamental data on price directions of related financial markets. At the same time, other technical analysts began exploring intermarket relationships too, most notably John Murphy, who has since authored an excellent book on the subject, entitled Intermarket Technical Analysis. However, these efforts, which identify whether this data is directly or inversely related to a specific market, still do not offer a way to quantify these relationships, or assess the simultaneous impact of multiple relationships on a given market.

Implementation
The appropriate tools needed to integrate data from related markets and quantify their influence on one another remained elusive until I began research into various artificial intelligence (AI) technologies. As it turns out, one of them, neural networks, is very well suited to implementing synergistic analysis. Neural networks can be used to synthesize technical, fundamental, and intermarket analysis into one analytic framework, capable of finding hidden patterns and complex relationships in data. The application of this technology to financial market analysis has quickly become a hot subject in the financial industry, with dozens of articles and several books written on the subject in the past few years. Amid all this hoopla, traders must keep this technology in perspective. Neural networks are simply a mathematical tool. It is their ability to quantify intermarket relationships and find patterns in data from related markets that allows neural networks to play an important role in implementing synergistic market analysis in today’s global markets.

SYNERGISTIC MARKET ANALYSIS WITH NEURAL NETWORKS
The remainder of this chapter will examine the application of neural networks to synergistic analysis. Traders who prefer to leave the research and development phase of neural networks to the experts, but who are interested in understanding how neural networks can be applied in their own trading right away, may want to skip to the section entitled “Implementation,” where I describe my firm’s neural network software program, called VantagePoint. This “turnkey” system, which requires no expertise in neural network development by the user, performs synergistic analysis to predict prices and trends for various financial futures markets.

For traders interested in what goes on “under the hood” of neural networks, the following sections will detail issues that must be addressed and potential pitfalls to be avoided when researching and developing financial applications with this technology. Emphasis will be on price and trend forecasting utilizing market data from a target market, related inter-markets, and fundamental inputs (see Figure 2). Attention will be focused on how to choose appropriate neural network paradigms, architectures, and training regimens for this type of application. Where appropriate, other artificial intelligence technologies will be discussed in terms of how they can be used in conjunction with neural networks to create hybrid information and trading systems.

ARTIFICIAL NEURAL NETWORKS
Artificial neural networks are loosely based upon models of how the human brain processes information. Neural networks utilize a distributed processing approach to computation, in which many simple processing elements, or neurons communicate with one another via a network. Information is stored in the network as a pattern of weights, and learning occurs during a training process in which changes are made to these weights. Neural networks are trained to behave in a desired fashion. Similar to humans, neural networks are capable of learning certain behaviors by being presented examples of those behaviors. Following training, neural networks are able to generalize to related but unseen behaviors.

Now let’s look at the following aspects of neural network development for financial forecasting:

• Paradigms
• Architecture
• Input data selection
• Preprocessing input data
• Fact Selection
• Training and testing
• Implementation

Paradigms
Neural networks are applicable to many general problem areas both within the financial industry, as well as in other industries. These areas include classification, filtering, autoassociation, pattern association, optimization, data compression and prediction. It is important to identify the problems to be addressed before starting to develop a neural network application, since the proper choice of network paradigm is dependent on the problem definition for a specific application.

For example, paradigms like differential competitive learning and counter-propagation can be used for data clustering tasks, while the Hopfield network and brain state in a box paradigms may be more appropriate for autoassociation, filtering, and pattern association. Each available paradigm has numerous variations, depending on how its parameters are selected. The problem domain of financial forecasting falls into the prediction category. For this application there are two often-used paradigms: recurrent back-propagation networks and feed-forward back-propagation networks. This chapter will focus on the latter, since it is probably the most widely used paradigm in financial analysis. Additionally, for every recurrent network there is a corresponding feed-forward network with identical behavior.

Feed-forward Back-Propagation Networks
A feed-forward network that trains by back-propagation of error throughout a multi-layered network is commonly referred to as a back-propagation, or back-prop, network. A typical back-prop network architecture is shown in Figure 3. In this type of network, time (temporal relationships) must be encoded into the facts presented to the network. To accomplish this a technique often referred to as taking a “snapshot” of the data is used to convert time-series data into a format necessary for training.

For example, to present facts that contain the differences in the closes for the past five weeks, a snapshot of the data must be created by constructing a fact with an input vector containing five values (one for each difference) and an output for the next week. This must be done for each fact-week to be presented to the network, effectively encoding the temporal information (data from the last five weeks) into the facts themselves.

Learning occurs in a feed-forward back-propagation network when it is given examples of inputs and expected outputs. For each output, the network computes an error measure between its generated output and the desired output. The error is typically averaged over the entire set of facts, then propagated backward through the network’s layers, and used to alter the weight connections between neurons. The weights are changed in this manner to reduce the overall error associated with the network’s outputs. As the training process continues, facts are presented to the network repeatedly in an effort to minimize the output error. While the error may be reduced to zero for simple problems, practical financial applications can not be expected to achieve this level of accuracy, as will be discussed later in this chapter.

Architecture

Some decisions that must be made in reference to network architecture are:

• What transfer function should be used?
• How many inputs does the network need?
• How many hidden layers does the network need?
• How many hidden neurons per hidden layer?
• How many outputs should the network have?

Back-prop networks are comprised of an input layer and an output layer, usually separated by one or more “hidden” layers. The hidden layers are not directly accessible to the network’s user. This arrangement, as represented in Figure 3, assumes that the layers are fully connected, which means that each neuron in the input layer is linked to each neuron in the hidden layer, with similar connections between the neurons in the hidden and output layers.

Each layer is comprised of neurons that send data to neurons in the next layer and receive data from neurons in the previous layer. The standard model is quite simple. For each neuron (see Figure 4), input data (I0-In) is multiplied by the weight (W0-Wn) associated with the connection to the neuron in the next layer. The products are summed, and the result is passed through a transfer function that maps the sum to a value in a specified interval, e.g., between zero and one . Each neuron’s output is then multiplied by another weight and fed into the next neuron. If this neuron is in the output layer, as is the case in Figure 3, the output is not multiplied by a weight but is instead the network’s output.

Transfer Functions
The transfer function, as mentioned earlier, maps a neuron’s inputs to an output. A neuron’s input signals are multiplied by their respective weights, summed, and then mapped via the transfer function to an output. It would not be appropriate, when modeling global financial markets, to use a transfer function which represents a line with a constant slope, or a discontinuous function, like those shown in Figure 5. Instead, the transfer function should be a nonlinear, continuously differentiable function, which allows the network to perform the necessary nonlinear modeling of interrelated financial markets.

The most commonly used nonlinear transfer functions include the logistic function (an example of which can be seen in Figure 4) and the tanh function, known as the hyperbolic tangent function. These functions are very similar to one another. The logistic function varies in height from zero to one, while the tanh function ranges from minus one to plus one.

Both of these functions can be used effectively in a back-prop network. Our research suggests that the tanh function trains slightly faster than the logistic function. Intuitively plausible reasons why this might be the case have been reported by other researchers.

Layers and Neurons
In addition to the choice of transfer function, it must be decided how many layers and how many neurons in each layer will be used. These decisions are relatively straightforward with respect to the input and output layers. For instance, in order to predict the change in the close for a particular futures contract based on a 20-day moving average of closes plus a five-day moving average of the high and a five-day moving average of the low, the network would require three input neurons and one output neuron. An example of such a net was depicted in Figure 3.

For nonlinear problems, such as predicting future prices of a stock or commodity, a back-prop neural network needs at least one hidden layer. There are no simple rules for determining the proper number of hidden layers in a back-propagation network. While one layer is theoretically sufficient to approximate any nonlinear function’s input-to-output mapping, networks can have more than one hidden layer. The best architectural configuration for a specific network application is usually arrived at through experimentation, since this facet of neural network development is more art than science. Experiments must be conducted to vary the number of hidden layers and hidden neurons to assess their influence on network performance. Complex problems typically require more hidden neurons. However, too many hidden neurons may cause “over-fitting” to the training data, which should be avoided since it may contribute to poor network performance later on.

The more task-specific a neural network is, the more easily it can be trained. Therefore, it is often preferable to design networks that have only one output, rather than having one network with two or more outputs.

In neural network development, no individual design decision, such as selecting the number of hidden layers or neurons, entirely determines how well the network will perform. Choice of input data, data preprocessing techniques, optimization of training parameters, and choice of testing procedures are all important factors that affect network performance. Since optimizing network architecture is time-consuming, due to the size of the parameter space to be explored, this process should be automated. The remainder of this chapter will examine these issues in more detail, and will illustrate real-world examples to highlight common pitfalls that should be avoided during each phase of neural network development.

Input Data Selection

Questions that must be answered during the input data selection phase of network development include:

• What is the problem domain?
• What are the input sources?
• Should the input sources be technical, fundamental, intermarket, or a combination of the three?

Data selection must be performed judiciously to avoid the “garbage-in, garbage-out” syndrome often associated with computers. A neural network’s performance is highly dependent on the quality and appropriateness of its input data. If relevant data inputs are not included, the network’s performance will suffer needlessly. For this reason it is important to have a solid understanding of the financial markets and intermarket relationships within the context of global trading.

Following a specific market analysis theory or analytic perspective on the markets when selecting input data for a financial neural network application has its own implications. I posit that the financial markets are nonlinear, and possibly chaotic that market inefficiencies exist, can be discerned quantitatively, and persist long enough for traders to profit from them. Technical analysis suggests the use of only single-market technical data as inputs. Fundamental analysis focuses on economic factors that influence the target market. Neither of these traditional approaches alone is sufficient in today’s global environment. Similarly, intermarket analysis that relies solely on the subjective and/or qualitative interpretation of several price charts cannot adequately model the simultaneous influence of multiple markets on a target market. By contrast, Synergistic Market Analysis, through the use of neural networks, combines these three methods of analysis into a multidimensional quantitative framework. Multiple data inputs reflecting a broad range of related markets and fundamental inputs can be used to discern the general tendencies and patterns between markets, and quantify these nonlinear relationships that affect a given market.

Now, to see how SMA can be implemented, let’s look at a simple example of input data selection for a neural network designed to predict the following week’s high and low for the Treasury bond market. First, technical price data on Treasury bonds is included to make general patterns and characteristics of the bond market apparent to the network. Then, related fundamental data, such as the federal funds rate, is included as additional inputs into the network. Finally, intermarket inputs are utilized. Sensitivity analysis, in which data inputs are varied, can be performed to help identify the best combination of intermarket and fundamental data to include as inputs.

For instance, in the case of VantagePoint, raw input data from the Treasury bond market — including open, high, low, close, volume, and open interest — is combined with similar data from eight related inter-markets — including the CRB Index, deutsche mark, Eurodollar, US Dollar Index, Japanese yen, S&P 500 Stock Index, crude oil, and gold. In addition, the daily Fed funds rate is included. Other VantagePoint systems incorporate inter-markets such as the FTSE and Nikkei stock indices as well as the Dow Jones Industrial and Utility Averages. Input selection and preprocessing is the subject of ongoing research by my firm, in an effort to improve network performance. Appendix 1 contains a simple case study that exemplifies the benefits of utilizing intermarket data.

Preprocessing Input Data

To facilitate neural network training, the selected raw input data must be preprocessed. Two widely used preprocessing methods, transformation and normalization, will now be discussed.

Transformation manipulates one or more raw data inputs to generate a single network input. Normalization is used to distribute data more evenly and scale it into an acceptable range for network usage. Decisions made during this phase are:

• What transformations should be applied to the data?
• Should these transforms include standard technical analysis indicators?
• How should the data be normalized?

As previously mentioned with respect to the selection of raw data inputs, domain knowledge is critical to the choice of preprocessing methods.

Transformation
For financial forecasting commonly used technical indicators like moving averages can be utilized as transforms. The noise component within raw price data tends to obscure underlying relationships between input data sources and slow down the training process. Therefore, smoothing techniques, such as moving averages, that help reduce the noise entering the network, are useful transforms.

In addition, two very simple preprocessing methods involve computing differences between, or ratios of, inputs. For example, when creating a neural net to predict the next week’s Treasury bond close, various length moving averages of the close can be used as inputs to the net. Additionally, moving averages of the ratio of the CRB Index to Treasury bond prices can be used as an intermarket input along with differences, or spreads, between Treasury bond prices and other related inter-markets. This helps to minimize the required number of input neurons and facilitates learning.

Normalization
The objective of data normalization is to ensure that the statistical distribution of values for each net input and output is roughly uniform. If this is not done, and an input with a normal distribution and a small variance is used, then the net will only see a small number of occurrences of facts away from the central tendency. The values should also be scaled to match the range of the input neurons. Therefore, in addition to any other transformations performed on network inputs, each should be normalized.

I will now discuss three useful methods of data normalization. The first is a simple linear method of scaling data. At a minimum, data must to be scaled into the range used by the network’s input neurons. This is typically in the range of minus one to one or zero to one. The scaling function involves finding the minimum and maximum values in a data set, setting these equal to the lower and upper values of the desired range, and scaling all intervening values based on the proportional change. This method scales input data into the appropriate range but does not increase its uniformity.

The second normalization method uses a statistical measure of central tendency and variance to help remove outliers, and spreads out the distribution of the data, typically increasing uniformity. This is done by altering, or clipping, data that is beyond a specified distance from the mean.

The third normalization method, the Mendelsohn histogram normalization (MHN) method, was developed by the Predictive Technologies Group, a research division of Market Technologies Corporation This function performs several transformations on the data to minimize the standard deviation of the heights of the columns in the initial frequency distribution histogram.

Figure 6 depicts an example distribution, in the form of a histogram, in which the data is not uniformly distributed. To illustrate the effects of the three methods of normalization, each has been used to prepare this data as input to a neural net in the range zero to one. Figure 7 shows that a simple linear scaling of the data has no effect on the shape of the frequency distribution itself. Figure 8 shows the same original distribution normalized by the second method, in which two standard deviations are used to set the limits for the outliers so that the distribution becomes more uniform. Figure 9 shows that, after performing MHN on the data, the resulting distribution is the most uniformly distributed. There are various methods that can be used to normalize data, with some methods being more effective than others, depending on the data to be normalized.

DENORMALIZATION
During the testing phase of development, the output produced must be denormalized. Ideally, the normalization should be reversible with little or no loss in accuracy. Normalization methods that clip outlier values are sometimes not sufficiently reversible. For instance, if during training all output values greater than 75 are clipped by assigning them a value of 75, then, during testing if the net produces an output of 75, this simply indicates that the output is 75 or more. If this level of detail is acceptable for a specific application, then the normalization method used is sufficiently reversible.

After the architecture has been selected, and the raw data inputs have been chosen and preprocessed, fact sets must be created.

Fact Selection
This section examines:

• What is a fact?
• What is a fact set?
• How many fact sets should be used in training a network?
• What criteria should be used to select facts for the fact sets?

A fact is a single input vector and its associated output vector. A fact is typically represented as a row of numbers where the first n numbers correspond to n network inputs and the last m numbers correspond to m network outputs. If a network has been designed to predict the change in price of the Dow Jones Industrial Average (DJIA) one week in advance, based on the differences in the highs and the lows for the past five days and a moving average of the closes for the past 10 days, then each fact would be composed of a three-valued input vector and a single-valued output vector. The three input values would correspond to the differences in the highs and the lows for the past five days and a moving average of the closes for the past 10 days. The single-valued output vector would represent the change in the DJIA over the next week (See Figure 10).

A fact set is a group of related facts. It is important to determine what data to include in a fact set, since it should represent the problem space to be modeled. For example, it must be decided whether or not to include S&P 500 data from October 1987 in a fact set. Since this data is not supported by a sufficient number of examples, the network may not be able to learn how to recognize it in the future. Additionally, its presence in the fact set might introduce a bias that could reduce the overall accuracy of the system during more typical trading periods.

Although internal technical data for a target market are readily available, related fundamental data are still not widely available through most data vendors. Likewise, relevant intermarket data may be unavailable, depending on when each of the related markets began trading. For instance, while Japanese yen futures began trading in 1972, the Nikkei 225 Index only started trading as a futures contract in 1990. To use both markets’ data in a neural network application for currency predictions, the fact set would have to be shortened so that it starts in 1990. However, use of shortened data sets can result in significant market characteristics being missed. For example, over the past decade there has really not been a sustained bear market in the S&P 500. Therefore, a neural network trained only on recent data will not be able to adapt quickly to changing market conditions in the future such as would occur at the onset of the next bear market. Data availability and sufficient representation of various market conditions are important considerations in the choice of input data and fact selection.

Training and Testing Fact Sets
Once the fact set has been selected, it is divided into training and testing subsets. Back-propagation networks operate in two modes: a learning or training mode, and a recall or testing mode. In the learning mode, the network modifies the values of its weights to adapt its internal representation, in an effort to improve the mapping of inputs to outputs. In the recall mode the network is presented with new inputs and utilizes the representation it had previously learned to generate associated outputs without changing the weights. Since neural networks operate in these two modes, the facts should be separated into at least two subsets: a training set and a testing set. The training set’s facts are used during learning, while the testing set’s facts are used during recall. Performance comparisons of various networks on the test set are used to determine which net to select for use in the final application.

Various criteria can be used to determine the composition of the training and testing sets. First, they should be mutually exclusive, which means that a specific fact does not reside in both subsets. It also means that if two facts have the same input and output values, one of these facts should be deleted from the fact set before it is separated into subsets. Additionally, caution must be exercised when using commercial tools that automatically split the initial fact set. For example, in an 80/20 split of the initial fact set, some tools may place every fifth fact in the test set, as opposed to randomly assigning facts to each subset. If the facts are in chronological order before the split, all data representing one day of the week, such as a Monday or Friday, could be assigned to the test set, while the remaining data would be assigned to the training set. This can skew the network results. To avoid this, the order of the facts should be randomized before they are split into subsets.

Even when randomizing fact order and splitting into subsets, all facts with a specific characteristic might still be placed in one subset or the other. To prevent this, it is advisable to identify the most important characteristics thought to be associated with the data and determine the fact set’s underlying distribution relative to these characteristics. Then the fact set can be split so that the training and testing subsets have similar distributions relative to these characteristics. Statistical analysis or clustering algorithms can be used to accomplish this. A careful analysis of the fact set will also allow outliers to be identified and eliminated.

Experimentation with a number of data-handling methods should be performed before selecting one. The Predictive Technologies Group has developed a training/testing regimen that splits the initial fact set into three mutually exclusive subsets, not just two. In addition to the standard training and testing sets, a second testing set, which includes examples of those facts thought to be most important in judging network performance, is utilized to compare various networks to one another.

Training And Testing
This section will examine the process of training and testing a back-propagation neural network. When performing these steps of network development, the following issues must be addressed:

1. How should the initial weights be determined?
2. What learning algorithm should be used?
3. What is the learning rate? How should it be set?
4. What is momentum? How should it be set?
5. What is simulated annealing?
6. What is over-training? How can it be avoided?
7. What metrics are appropriate for testing?

After the training fact set has been created, training can be initiated. First, the weights are initialized. Typically, relatively small random weights are used to initialize the network. As mentioned earlier, during training the weights are changed to allow the network to adapt its internal representation when modeling a problem. It is sometimes advisable to train the same network several times with different sets of initial weights, since they can affect network training and performance.

Learning Algorithms
Various learning algorithms can be used when performing back-propagation, which provide methods of minimizing the overall error associated with the network’s output. They accomplish this by traversing the net’s error surface, or error landscape. Since the landscape is immense, each algorithm attempts to minimize the overall error while evaluating as few points as possible on the error surface. This results in a trade-off between network performance and training time. If every point on the surface were to be evaluated through an exhaustive search, optimal performance would be assured. Since this would be impossible for all but the simplest problems, algorithms are utilized that produce acceptable solutions within a reasonable time.

The Gradient-Descent Algorithms
One of the most common algorithms used in back-propagation is the gradient-descent algorithm. Starting at an initial point on the error surface, it determines the gradient that quantifies the slope, or steepness, of the curvature of the error surface at that point. The algorithm uses this information by moving in the exact opposite direction by an amount proportional to the learning rate, a constant discussed later in this chapter. By utilizing this “downhill” movement along the error surface, the algorithm minimizes error.

Other learning algorithms include conjugate-gradients, Newton-Raphson and Levenberg-Marquardt. However, no one algorithm is the best for all optimization problems. They all require a starting point somewhere in the vicinity of the optimal point, and some degree of smoothness of the performance landscape. This is not true of genetic algorithms.

Genetic Algorithms (GAs)
Genetic algorithms use simple mechanisms, analogous to those used in genetics, to breed populations of superior solutions. Those that do well “breed” with other solutions to form new solutions. Solutions that perform poorly are culled.

Genetic algorithms are a robust class of optimization algorithms. They do not require any special initial conditions and make no requirements on the smoothness of the performance landscape.

Genetic algorithms can be used to train a net by evolving populations of weight matrices. In this case, back-propagation of errors is not needed. Only the forward-propagation of facts through the net and subsequent evaluation of the fact-errors is required.

Learning
The network “learns” during training by altering its weights, based on error information propagated backward throughout the network from the output layer. Error can be propagated, and weights changed, each time a fact is presented, after a subset of the facts has been presented, or after all facts have been presented. One cycle, in which all facts have been presented to the network, is referred to as an epoch. With each change in the weights’ values, the network is taking a step on a multidimensional surface, which represents the overall error space. During training, the network traverses the surface in an attempt to find the lowest point, or minimum error. Weight changes are proportional to a training parameter called the learning rate.

Oscillation
The largest possible learning rate that does not result in oscillation should be selected. As a simple example of oscillation, imagine that a network’s current weight values place it halfway down a valley on a two-dimensional error surface, as depicted in Figure 11. If the learning rate is too large, the network’s next step might be to the other side of the valley, as opposed to moving toward the bottom. Then, the following step might return to the original side, so that the network tends to bounce back and forth from one side of the valley to the other without much movement toward the bottom, where the solution lies. Alternatively, with too small a learning rate, in which the steps that the network takes are very small, it could take too long to get to the bottom of the valley to arrive at a solution. Since each problem space has its own unique error surface, the learning rate must be varied to achieve the best balance between training time and overall error reduction for a specific application.

Momentum
Another training parameter, known as momentum, acts as a filter to reduce oscillation. It allows higher learning rates to be used to obtain solutions similar to those found with lower learning rates, thereby potentially decreasing the training time. Learning rates and momentum should be adjusted through experimentation. Some development tools include additional parameters — such as temperature, gain, and noise — that can also be modified to affect training.

Simulated Annealing
Simulated annealing is a training method that simulates the process of annealing by including a temperature term which affects the learning rate. The temperature begins relatively high, allowing the network to move quickly over the error surface. Then, as training progresses the temperature decreases, so that learning slows as the network cools and settles upon a near-optimum solution. The use of simulated annealing also reduces the likelihood of oscillation. Figure 12 depicts a two-dimensional example of simulated annealing, in which the step size is reduced to avoid oscillation while finding a minimum point on the error surface.

Training and Testing Automation Necessary
The multidimensional space defined by all free parameters is known as the parameter-space of a back-propagation model. If it has only two free parameters, such as the learning rate and the momentum, then the parameter-space can be represented graphically in two dimensions with the learning rate on one axis and the momentum on the other. Here, the parameter-space is composed of the quarter-plane defined by the positive values of the two parameters (See Figure 13).

The goal is to find an optimal set of values for the parameters, whereby an optimally performing net is produced upon training with these values. This amounts to finding the “best” point in the parameter-space.

Brute-Force
Brute-force is perhaps the simplest way to find the optimal parameters, in which a large set of points in the parameter-space is examined. Assume that a third axis representing performance is defined. The three-dimensional space comprised of the learning rate, momentum and performance can be viewed as creating a performance landscape. Each experiment identifies one point on the performance landscape. Once many points have been identified, the shape of the landscape becomes apparent (at least in this simple example). Now, the landscape can be used to guide the selection of trial parameter-space points.

After investigating the properties of the back-propagation paradigm, a practical sense of the size of its parameter-space can be appreciated. The training parameters may vary from node to node in the network and from epoch to epoch during training. If a net has 100 trainable nodes and is trained for 1,000 epochs, then the two-dimensional example becomes 200,000-dimensional!

To further complicate matters, all possible initial (random weight) conditions, as well as the number of hidden layers and nodes, must be considered part of the parameter-space. In this light, the parameter-space is virtually infinite in extent.

Automation
The myriad decisions that must be made in the development of a neural network application makes automation of the training and testing process highly desirable. This is particularly true in selecting preprocessing, choosing the number of hidden layers and neurons, and setting training parameters. Tools such as genetic algorithms can be used to expedite parameter space searches. Genetic algorithms can be used to control only the free parameters, such as the learning rate and momentum within the traditional gradient-descent based back-prop algorithm. Also, methods such as simulated annealing are useful for automating learning rate adjustments during training.

Avoid Over Training
During training, a serious pitfall that must be avoided is over-training. This is analogous to the common problem of over-optimizing rule-based trading systems. Over-training occurs when a network has learned not only the basic mapping associated with the input and output data presented to it, but also the subtle nuances and even the errors specific to the training set. Through memorization, an over-trained network can perform very well on the training set, but fail to do so on out-of-sample test data and later during actual trading. This is because the network is unable to generalize to new data.

Over-training can be avoided through the use of an automated training/testing routine in which testing is an integral part of the training process. Network training is stopped periodically at predetermined intervals. The network then operates in recall mode on the test set to evaluate the network’s performance on selected error criteria, after which training resumes.

This process continues iteratively, with interim results that meet selected error criteria retained for later analysis. When network performance on the test set begins to degrade, the best saved network configurations up to this point are further evaluated. In order to conduct a rigorous comparison of various networks as their architectures, raw data inputs, preprocessing, and training parameters are changed, a robust, automated training/testing methodology is necessary.

Error Measures
Network performance can be evaluated on test data according to various criteria. One commonly used error measure is called average error. Unfortunately, when judging network performance, this metric is not particularly useful, since the positive errors cancel the negative errors. A more useful error metric would be average absolute error. With this metric, the absolute value of the error for each fact in the test set is summed and then divided by the number of facts in the test set. Examples of other error measures based on the distance from the target value include sum-of-squares error and root mean squared (RMS) error.

Neural networks can even be used to judge the performance of other networks. One simple approach that we use to determine how much a net can still be improved is to train a second net which predicts the errors of the first net. If the second net learns to predict a significant percentage of the first net’s errors, then the first net could still be improved. This method is referred to as iterative refinement, since it may be repeated indefinitely by adding more nets. There are other approaches that are useful for improving a net’s performance, but most involve constructive algorithms applied during the training or retraining of an existing net.

Expectations of Performance
Performance expectations for a financial forecasting application depend on one’s viewpoint of the underlying market dynamics of the target market. For example, if a neural net is designed to forecast a completely random time series, then it should not be surprising if large prediction errors occur, since, by definition, such a time series is unpredictable.

While a given market is driven by both stochastic (random) and deterministic forces, only the latter are predictable. However, even chaos can be deterministically generated. As recent work at Los Alamos National Laboratory has shown, neural networks can predict such chaos quite well.

Still, expectations must be realistic. The equity curve in Figure 21 (from the section on “Hybrid Trading Systems”) based on VantagePoint’s predicted information, suggests that there is a sufficient degree of predictability within the markets to be profitable. Presently, the maximum achievable accuracy of financial forecasting is unknown. It is unrealistic to expect to achieve zero error, since this would require a model that accounts for events that are today deemed random. Nevertheless, simply because events are currently unpredictable does not mean that they are necessarily random. Indeed, each revision of VantagePoint over the past three years has been able to predict events that previously appeared to be stochastic noise. For the time being, it is unknown where the “ceiling” on performance accuracy is located.

Since many commercial network development tools have limited error metrics available, development and implementation of custom error functions is most desirable for serious network development.

Successful neural network applications for nontrivial problems require considerable talent and expertise in a number of disciplines, including market analysis, computer science, and applied mathematics. Even with extensive in-house research and development tools and availability of numerous commercial tools, neural net development to implement Synergistic Market Analysis for financial forecasting is a time-consuming, labor-intensive task. Since a team effort is necessary for successful neural network development, traders lacking such expertise can still benefit from this technology’s ability to assess intermarket relationships through the application of fully developed and trained networks, such as VantagePoint. The main benefit of utilizing a pre-trained neural network system is that traders can put this technology to use without having to first become rocket scientists.

Implementation
Now I would like to discuss how Synergistic Analysis can be implemented through the use of neural networks, and how they can be integrated within an overall trading strategy into two types of trading applications: information systems and trading systems. VantagePoint will be used as an example to illustrate how this can be accomplished. Finally, I will offer insights into future directions for use of artificial intelligence technologies to implement Synergistic Market Analysis in the financial forecasting arena.

Information Systems
Information systems that generate forecasts related to a specific target market, including price forecasts and predictions about market direction or turning points, can be implemented through the use of neural networks. Such information can be used alone or in conjunction with other analytic information available to the trader. Information systems can be comprised of a single neural network, or as in the case of VantagePoint, which utilizes five networks, a multi-network hierarchically organized system. Traders need to collect daily data on the target market and related inter-markets by modem, in order to obtain predictions for the next day’s trading.

VantagePoint has four networks, which are specifically designed and trained to make independent market forecasts of the high, low, short-term, and medium-term trends for use on the following trading day. Since these forecasts are independently derived, they can be used to confirm one another. Additionally, the outputs from the four networks are used as inputs into a fifth network, which predicts market turning points. A network architecture such as VantagePoint’s, depicted in Figure 14, is referred to as hierarchical.

In this type of network configuration, predictions made by networks at the primary level of the hierarchy are incorporated as inputs into a network, or networks, at a secondary level. Such hierarchical architecture facilitates faster training, since all networks at the primary level of the hierarchy can be trained simultaneously, as each focuses solely on a single output.

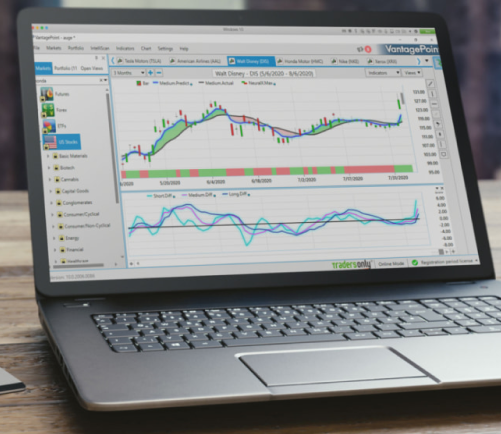
VantagePoint’s predictions can be visualized graphically with various chart overlays or in tabular form on its daily trading prediction report. When viewing the charts, users can select four different chart types, from bar charts to candlestick charts (See Figure 15). As many as eight different studies can be overlayed on each chart. These studies include both forecasted information as well as information computed from these forecasts, to help traders utilize the information more effectively. Additionally, to customize the chart’s appearance, a variety of user-adjustable parameters (See Figure 15) are available.

An example of a chart produced by the VantagePoint Treasury Bond System is shown in Figure 16, in which the predicted high and low values are plotted over the daily price bars. Such information is particularly useful in helping to determine entry and exit points for day trading or position holding. If the forecasted information on the daily report suggests that the next day will be an up day in the market, day traders might wait until the market trades down toward the predicted low, then enter a long position with a limit or market order. The reverse would involve entering a short position at or near the predicted high on a day expected to be a down day. Entering at these levels increases the potential for a profitable day trade. Two examples of this are shown from the March 1994 Treasury Bond contract (See Figure 17). In the example on the left, the up arrow (indicating an expected upward trend in market direction) and the predicted low for tomorrow are generated on December 2, 1993. If a long position was entered on the open and exited at the close on December 3, 1993, based solely on the anticipated direction, a profit of 12 ticks ($375.00 before slippage and commission) would have been realized. If, instead, an entry to go long had been executed at the predicted low, with an exit at the close, a profit of 24 ticks ($750.00 before slippage and commission) would have been realized, doubling the profit.

The example on the right of Figure 17 shows the same concept in reverse. Instead of entering at the open and exiting at the close on an expected down day, a short trade could be entered at the predicted high and exited at the close, resulting in a profit of 10 ticks ($312.50 before slippage and commission). Additionally, day traders can use the predicted high/low range to set exit points, rather than exiting at the close. In this scenario, on a day when the market direction is predicted to be up, a long position is entered at or near the predicted low, then closed out intraday at or near the predicted high. Similarly, short positions can be closed out intraday at or near the predicted low, rather than exited at the close.

Using these strategies, entry trades may not get executed when the market does not make the entry objective indicated by the predicted high or low. However, the profitability of those trades that are executed can be substantial, with minimal risk since very tight stops can be used.

Position holders might apply the same principles in entering the market, using the predicted range on subsequent days to set daily stops. For example, if position holders are long Treasury bonds and the next day is expected to be an up day, they might set their stops for the next day a few ticks below its predicted low, which acts as a support level. This reduces the likelihood of getting stopped out during the day prematurely as the result of intraday market volatility, yet protects profits in the event of a severe intraday market downturn.

Position holders and day traders can use forecasted trends and changes in trend direction to their advantage. This information can be used alone or in conjunction with other market information to generate buy/sell signals. One still popular method of technical analysis is a moving average crossover system. Typically, two or more moving averages are plotted on a chart. Buy and sell signals are generated when the short moving average crosses over or under the long moving average. The obvious limitation of this approach is that, by definition, moving averages are lagging indicators. As a result, they get whipsawed during sideways markets. Moving average systems also generate signals after market turning points have occurred, thus sacrificing profits at the beginning and end of a market move. Neural-network-generated trend forecasts can be used effectively by traders to reduce the lag associated with a traditional moving average crossover system. Instead of using a calculated value for today’s short moving average, a forecasted moving average value for two to four days into the future can be used as the short moving average, in a crossover system. This reduces the lag, since the short moving average is now a prediction of its value at a later point in time, instead of today’s calculated value. An example of a move captured by the crossover of a forecasted 10-day moving average four days in the future against a calculated 10-day moving average today is shown, as it would appear in VantagePoint, in Figure 18.

VantagePoint has adjustable parameters that allow users to customize the system to their style of trading. Figure 19 depicts a sample screen containing customizable parameters. Users can emphasize the importance placed on each of the predictions in affecting the Strength Index which measures the strength of the impending move. This is done by altering the various “Weight” parameters. Signals that indicate the general market movement (up, down or sideways) are then generated by filtering the Strength Index by the “Upper Strength Limit” and “Lower Strength Limit”. In addition, other parameters can be set by traders to further customize VantagePoint’s information.

Trading Systems
Neural networks can also be utilized in other ways. They can be trained to forecast trading signals. This is appealing, but has limitations which must be understood. Designing such a system requires that the trader who is actually going to use it be involved in its development. Since the network will generate its trading signals based on the buy/sell points and the choice of selected input data and preprocessing performed during development, the signals must be consistent with the trader’s style, risk propensity, investment time horizon, and capitalization.

Since traders have different trading styles, even with perfect hindsight no two traders would identify the same buy/sell points on historical data. Therefore, traders who are unable to tolerate large drawdowns would not develop a neural network that generates signals more appropriate for traders with larger capitalization or a higher risk propensity. Additionally, it is not easy to incorporate risk management considerations into a purely neural-network-based trading system. For this reason, a neural network is best utilized as an information system, or as part of a hybrid system, in conjunction with some sort of rule-based algorithms.

Hybrid Trading Systems
When used as part of a hybrid system, the neural network generates predictive information that can be used along with a set of rules that generate trading signals (see Figure 20).

This approach combines a front-end information system with a back-end rule-based system. The rule-based portion of the system could range the gamut from relatively simple mathematical constructs to sophisticated expert systems. Regardless of how they are derived, the rules would need to be tailored to the trading style of the trader who will use the system.

Now let us examine how an information system, such as VantagePoint, can be used as part of a hybrid trading system. VantagePoint would represent the box labeled “Information System” in Figure 20. For the box labeled “Rules” we have devised a simple set of rules that utilize VantagePoint’s predicted information to generate buy and sell signals. This particular system uses just some of the information generated each day by VantagePoint’s Treasury bond system, including the short and medium market, which are two user adjustable indicators based on the various forecasts produced by VantagePoint. The short and medium market generate up, down and sideways arrows on VantagePoint’s charts, indicating the market trend direction for up to four trading days in the future.

If two up or down arrows occur within a specified window in the medium market, the system takes a long or short position, respectively, on the following day. Timing decisions concerning whether to enter at the open with a market order, or to use a limit order, in conjunction with VantagePoint’s predicted high and low for a more advantageous entry, are left to the trader’s discretion. A full description of the details of this system can be found in APPENDIX 2 at the end of this chapter, along with a trade listing and summary of simulated trades made on the December 1992, March 1993, June 1993, September 1993, December 1993, March 1994, and June 1994 Treasury bond futures contracts, trading one contract at a time. Simulated trading of the system over these contract months (over 1.5 years of trading) resulted in the equity curve shown in Figure 21.

This chapter has briefly discussed all phases of neural network development, including decisions involving network architecture, input selection, preprocessing, fact selection, training, testing and implementation. Each of these phases has been examined in the context of the recent globalization of the world’s financial markets and the need to establish a synergistic framework to quantitatively assess technical, fundamental, and intermarket data. While an in-depth discussion of the development of an actual neural network system, such as VantagePoint, is beyond the scope of this chapter, a simple case study that utilizes some of VantagePoint’s features can be seen in APPENDIX 2.

WHAT’S NEXT
Neural networks are an excellent tool for combining otherwise disparate technical, fundamental, and intermarket data within a quantitative framework for implementation of Synergistic Analysis. Through the use of neural networks, nonlinear patterns and intermarket relationships can be ascertained. In the global markets of the 1990s, it is dangerous to ignore this critical information by focusing only on a single market at a time. As market globalization accelerates and more traders recognize the benefit of a synergistic approach to global market analysis, technical analysis as it is currently practiced will become totally obsolete. Synergistic Analysis, combining technical, fundamental, and intermarket perspectives, will emerge as the preferred analytic framework for trading.

Still, it must be realized that neural network technology is just one of the tools applicable to the implementation of a synergistic trading strategy. Other related technologies, including expert systems and genetic algorithms, have a role to play in implementing Synergistic Analysis for financial forecasting. In fact, neural networks can be used to help extract primitive rules, which capture patterns that would not be apparent otherwise, for incorporation into an expert system.

Genetic algorithms are powerful search mechanisms which are well suited to optimizing neural network parameters. As mentioned earlier, during training, genetic algorithms can be used as a training algorithm or to search the space of training parameters in an efficient manner. Genetic algorithms can also be used to automate the search for an optimal set of raw inputs and appropriate preprocessing, so that these tasks can be performed efficiently.

The same technology incorporated into genetic algorithms has also been used in classifier systems and genetic programming. Classifier systems perform a type of machine learning that generates rules from examples. Genetic programming goes even further by automatically generating a program from a set of primitive constructs. In addition to genetic models, fuzzy logic, wavelets, and chaos are also being applied in a multitude of domains including financial forecasting. Even virtual reality has applicability to financial analysis.

Advancements in hardware are also affecting the speed at which various artificial intelligence technologies will be applied to financial market analysis, since these technologies are computationally intensive. In particular, massively parallel machines will be beneficial in this regard. Parallel processing machines work on different parts of a single problem simultaneously. As a result, the computing time associated with solving a particular type of problem is substantially reduced, once a suitable method of dividing the problem is devised. Neural networks and genetic algorithms are well suited to these parallel processing machines. With connectionist machines, accelerator boards, hypercube architectures, etc., hardware advancements will further facilitate the application of emerging software technologies to financial market analysis.

Although this chapter’s focus has been on the application of SMA and neural networks to financial forecasting, their applicability goes far beyond this single arena. One area where my firm has been performing research is that of global asset allocation. Synergistic Analysis can be used to reduce diversifiable risk in global portfolio management by generating forecasts required by an asset allocation model. By using SMA and neural networks to increase forecasting accuracy, portfolios can be constructed and rebalanced that provide higher return for equivalent risk, or lower risk for equivalent return. Other technologies, such as expert systems, can be used to measure investor characteristics such as risk propensity.

Over the next decade, researchers will continue to explore the application of these technologies to financial market analysis and develop complex hybrid systems. In the meantime, individual traders need to give more than just lip service to the globalization of markets and must move beyond the narrow focus of today’s single-market analysis in order to analyze the interrelationships of markets and benefit from such information. Traders with the foresight to adopt a broader market perspective that encompasses today’s intermarket global context will gain a competitive advantage over their competitors who continue to limit the focus of their analysis. The sooner traders adjust their thinking about technical analysis, and begin to benefit from more robust analytic methods and tools that employ a synergistic framework for intermarket global analysis, the more successful, disciplined, and confident their trading will become.

Easy-to-use software programs such as VantagePoint, which open the door of intermarket analysis to individual traders, while leaving the research and development of neural networks to professional developers, are an ideal way for traders to bridge the gap in their technical analysis arsenal and to begin benefiting immediately from global trading. In warfare, having more advanced weapons than one’s opponent is a decided advantage. The same principle applies to the tools that traders use in the highly volatile global financial markets of this decade. Synergistic Analysis through the use of neural networks is one very powerful tool that should be part of every serious trader’s arsenal.

The author would like to thank James T. Lilkendey, M.S. and Phillip Arcuri, Ph. D., of the Predictive Technologies Group, for their assistance in preparation of this chapter.

Synergistic Market Analysis, Market Synergy, Synergistic Analysis, and Synergistic Trading are trademarks of Lou Mendelsohn.

REFERENCES

1 Eiteman, D. K., Stonehill, A. I. & Moffett, M. H. [1992]. Multinational Business Finance, Addison-Wesley Publishing Company.
2 Diamond, B. B. & Kollar, M. P. [1989]. 24-Hour Trading: The Global Network of Futures and Options Markets, John Wiley & Sons.
3 Ibbotson, R. G. & Brinson, G. P. [1993]. Global Investing: The Professional’s Guide to the World Capital Markets, McGraw-Hill, Inc.
4 Levine, S. N. [1992]. Global Investing: A Handbook for Sophisticated Investors, HarperBusiness.
5 Mendelsohn, L. B. [1990]. “Building a Global Safety Net,” The Journal of Commerce, Feb. 5, 1990.
6 Mendelsohn, L. B. [1990]. “24-hour trading: Let’s do it right,” Futures, April 1990.
7 Mendelsohn, L. B. [1989]. “It’s Time to Combine Fundamental and Technical Analysis for a Total Game Plan,” Barron’s, March 13, 1989.
8 Mendelsohn, L. B. [1983]. “Picking software programs: Know their limitations,” Commodities (Futures), May, 1983.
9 Mendelsohn, L. B. [1983]. “History tester important factor in software selection,” Commodities (Futures), July, 1983.
10 Murphy, J. J. [1991]. Intermarket Technical Analysis, John Wiley & Sons, Inc.
11 Mendelsohn, L. B. [1991]. “The Basics of Developing A Neural Trading System,” Technical Analysis of Stocks & Commodities, June, 1991.
12 Chinetti, D., Gardin, F. & Rossignoli, C. [1993]. “A Neural Network model for Stock Market Prediction,” The Second International Conference on Artificial Intelligence Applications on Wall Street.
13 Jang, G. & Lai, F. [1993]. “Intelligent Stock Market Prediction System Using Dual Adaptive-Structure Neural Networks,” The Second International Conference on Artificial Intelligence Applications on Wall Street.
14 Trippi, R. R. & Efraim, T. [1992]. Neural Networks in Finance and Investing: Using Artificial Intelligence to Improve Real-World Performance.
15 Hecht-Nielsen, R. [1990]. Neurocomputing, Addison-Wesley Publishing Company, Inc.
16 Aleksander, I. & Morton, H. [1990]. An Introduction to Neural Computing, Chapman and Hall.
17 Wasserman, P. D. [1989]. Neural Computing: Theory and Practice, Van Nostrand Reinhold.
18 Hecht-Nielsen, R. [1990]. Neurocomputing, Addison-Wesley Publishing Company, Inc.
19 Gallant, S. I. [1993]. Neural Network Learning and Expert Systems, The Massachusetts Institute of Technology.
20 Peters, E. E. [1991]. Chaos and Order in the Capital Markets: A New View of Cycles, Prices and Market Volatility, John Wiley & Sons.
21 Peters, E. E. [1994]. Fractal Market Analysis: Applying Chaos Theory to Investment & Economics, John Wiley & Sons.
22 Wolfe, M. A. [1978]. Numerical Methods for Unconstrained Optimization: An Introduction, Van Nostrand Reinhold.
23 Holland, J. H. [1975]. Adaptation in Natural and Artificial Systems. Ann Arbor: The University of Michigan Press.
24 Goldberg, D. E. [1989]. Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley Publishing Company.
25 Gallant, S. I. [1993]. Neural Network Learning and Expert Systems, The Massachusetts Institute of Technology.
26 Lapedes, A. & Farber, R. [1987]. “Nonlinear Signal Processing Using Neural Network Prediction and System Modeling,” Theoretical Division, Los Alamos National Laboratory, Report #: LA-UR-87-2662.
27 Farmer, D. F. and Sidorowich, J. J. [1988]. “Exploiting Chaos to Predict the Future and Reduce Noise,” Version 1.2. Theoretical Division, and Center for Nonlinear Studies, Los Alamos National Laboratory, Report #: LA-UR-88-901.
28 Gallant, S. I. [1993]. Neural Network Learning and Expert Systems, The Massachusetts Institute of Technology.
29 Colin, A. M. [1992]. “Neural Networks and Genetic Algorithms for Exchange Rate Forecasting,” International Joint Conference on Neural Networks, Beijing, China, Nov. 1-5.
30 Deboeck, G. J. [1993]. “Neural, Genetic and Fuzzy Approaches to the Design of Trading Systems,” The Second International Conference on Artificial Intelligence Applications on Wall Street.